My previous blog covered the mathematics involved in the neural network that we are going to write. You can find it here. The ideas covered in the blog are used, but a complete understanding is not necessary for reading this blog.
You can find the code from the repository, juxt/prop.
Starting the Neural Network
What are our initial variables for the construction of a neural network?
-
Inputs
-
Outputs
-
Bias on each neuron
-
Bias weights
Some of you may be thinking, we also need the weights right? Isn’t that the whole point of a neural network… to update the weights in order to get your desired output? You are absolutely correct, the weights are updated through each iteration. That is the precise reason why we don’t initially specify the weights, as they are going to change, so we may as well start with a random number, between -1 and 1.
In nn we create our initial network with the random weights generated.
(defn nn [input output output-bias & args]
(let [num-bias (into [] (for [arg args] (:num arg)))
hidden-weights (->> num-bias (partition 2 1) (mapv (partial reduce rep)))
output-weight (conj hidden-weights (rep (-> args last :num) (count output)))
weights (cons (rep (count input) (-> args first :num)) output-weight)]
{:input input
:bias (to-vector output-bias args vals)
:weights (into [] weights)
:bias-weights (conj (vec
(for [arg args]
(vec (butlast (keys arg)))))
(-> output-bias keys vec))
:output output}))We define our neural network using the above function as follows:
(def network (nn [1 0 1]
[0.1 0.5]
{0.3 0.6 0.4 0.8}
{0.05 0.1 0.15 0.2 :num 2}
{0.25 0.3 0.35 0.4 :num 2}))Feed Forward Pass
Next we calculate the sigmoid values. We use the sigmoid values of the previous layer, the bias, weights and bias-weights.
(defn calc-sigmoid [{:keys [input bias weights bias-weights output]}]
{:sig-values (loop [ind 1
res [(sigmoid-layer input (first weights) (first bias) (first bias-weights))]]
(if (>= ind (count bias-weights))
res
(recur (inc ind)
(conj res (sigmoid-layer (last res) (get weights ind) (get bias ind) (get bias-weights ind))))))
:output output})In this calculation we use core.matrix to calculate the net of every neuron in each layer.
(defn net-layer [inputs weights bias bias-weights]
(M/+
(m/mmul
(m/matrix [inputs])
(m/matrix weights))
(M/*
(m/matrix [bias])
(m/matrix [bias-weights]))))The result is passed into the sigmoid function to get the values of the neurons in each layer.
(defn sigmoid-layer [inputs weights bias bias-weights]
(mapv sigmoid (first (net-layer inputs weights bias bias-weights))))At this stage we have the sigmoid values of every neuron and are able to calculate the error on each neuron and the total error, which is the sum. The target is the output, and the output-sigmoid is the final vector of calc-sigmoid.
(defn output-error [target output-sigmoid]
(* 0.5 (- target output-sigmoid) (- target output-sigmoid)))Updating the weights
Now we get to the most interesting and difficult process in calculating the new weights. To do this we have to recognize that each weight depends on certain variables. So all we need to do is get these variables.
I have used the premise that a weight connects two neurons.
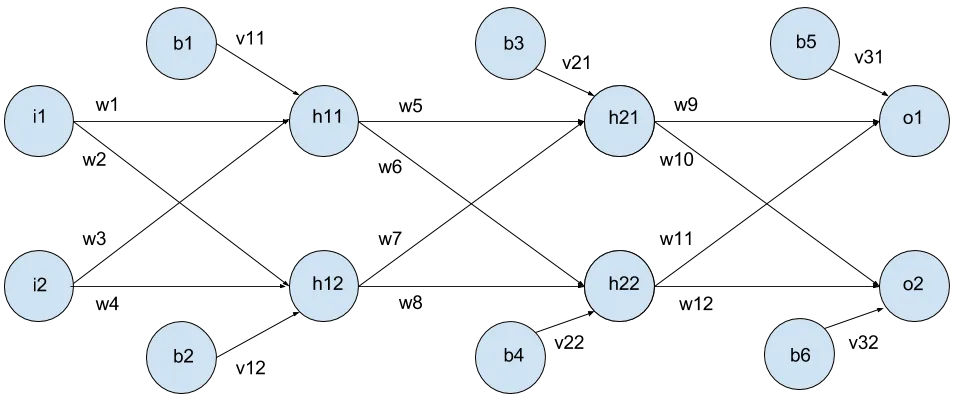
As you can see, weight w1 connects neuron i1 to neuron h11. First we want to get vectors of these links.
Linking the Neuron
(defnp links [{:keys [input bias weights bias-weights output] :as network}]
(let [sig (cons input (:sig-values (calc-sigmoid network)))]
{:weight-links (mapv #(connector (vec sig)
weights
(p :links-first-first (-> % first first))
(-> % first second)
(-> % first last))
(mapv #(indexer weights %) (flatten weights)))
:sig sig}))Going back to

The neuron values are in a vector
[[i1 i2] [h11 h12] [h21 h22] [o1 o2]]The weights are in the vector
[[[w1 w2] [w3 w4]]
[[w5 w6] [w7 w8]]
[[w9 w10] [w11 w12]]]w1 connects i1 and h11. w2 connects i1 and h12.
The index of w1 in weights is [0 0 0]. The i1 in values is [0 0] and h11 is [1 0] The index of w2 in weights is [0 0 1]. The i1 in values is [0 0] and h12 is [1 1] …
Therefore using the index of the weight, if we say the index of w1, [0 0 0] = [a b c], the the index of i1 is [0 0] = [a b]
and the index of h11 is [1 0] = [(+ a 1) c].
We can see this working with w2. [0 0 1] = [a b c]. i1 is [0 0] = [a b]. h12 is [1 1] = [(+ a 1) c]
Prove to yourself with the other weights to see why this works.
We use the connector function to generate these links.
(defn connector [values weights a b c]
[(reduce get weights [a b c])
(reduce get values [a b])
(reduce get values [(+ 1 a) c])])Finding the Variables
Before we can calculate the delta, we first need the variables.
(defn delta-variables [weight network links*]
(let [{:keys [weight-links sig]} links*
output-sig (last sig)
connect (list (connection weight weight-links))]
{:delta-variables (if (p :some (some #(= (-> connect first first last) %)
output-sig))
(mapv rest (first connect))
(p :loop (loop [res (mapv rest (first connect))
c connect]
(let [new-c (first (map (fn [x]
(map (fn [cc] (let [woutput (last cc)
woutput-links (connection woutput weight-links)]
(filter #(= (get % 1) woutput) woutput-links)))
x))
c))
new-res (conj
res
(map (fn [x]
(map (fn [xx]
[(first xx) (last xx)])
x))
new-c))]
(if (some #(= (-> new-c first first last) %) output-sig)
new-res
(recur new-res
new-c))))))
:last-sig output-sig}))This function doesn’t look pretty, and I will be the first to admit that it can be improved. The underlying theory is a weight links neuron A to B. We check if neuron B is in the final layer, i.e. the output layer. If it is, we take the values of the two neurons.
If neuron B is not in the final layer, we still take the values of the two neurons, but, look further at neuron B and get all links where neuron B acts as neuron A, the first neuron. We then check if the new neuron B is the output layer. If it is, we take the weight and the new neuron B. If not, we repeat the process.
Calculating Delta
(defn delta-value [weight {:keys [output] :as network} links*]
(let [{:keys [delta-variables last-sig]} (p :delta-variables (delta-variables weight network links*))
first-vars (first delta-variables)
last-vars (last delta-variables)
middle-vars (butlast (rest delta-variables))
a (layer-eq first-vars)
b (map (fn [x] (map (fn [xx] (output-eq xx output last-sig)) x)) last-vars)
c (map (fn [x] (map (fn [xx] (map (fn [xxx] (layer-eq xxx)) xx)) x)) middle-vars)]
(cond
(and (nil? middle-vars) (= first-vars last-vars)) (output-eq last-vars output last-sig)
(nil? middle-vars) (* a (first (map #(apply + %) b)))
:else (p :cond3 (* a (first (map #(apply + %) (reduce (fn [acc v] (M/* v (map #(apply + %) acc))) b (reverse c)))))))))Calculating the delta now becomes relatively straightforward as we have the variables and we know the formulae from the Mathematics Blog.
We have to use special cases depending on the layer though. I am going
to call the output layer the top layer, and the input layer the bottom
layer. From the cond, the first condition is the first layer from the
top, the second condition is the second layer from the top and then we
arrive at the general case.
Arriving at the New Weight
(defnp new-weight [weight network learning-rate links*]
(let [new-value (delta-value weight network links*)]
(- weight (* learning-rate new-value))))To calculate the new weight, we multiply the delta-value with the learning rate and take that away from the original weight. Doing this to all the weights gives us a new set of adjusted weights for our next iteration.
ITERATE
The final step is the iterations. Here we use a simple loop and add some
printlns to keep track of the neural network while it is running.
(defnp train [network learning-rate num-of-iterations println?]
(loop [x 0
v network]
(if (>= x num-of-iterations)
v
(recur (inc x)
(let [{:keys [new-weights]} (new-network-weights v learning-rate)]
(when println?
(println "Total error is: " (:total-error (-> v calc-sigmoid errors)) "Iteration is: " (inc x)))
(assoc v :weights new-weights))))))Playing with the network
The neural network is available for you to use in your projects, found here
Also, please note that future versions of the code may vary in order to optimize performance. However, this blog contains the core ideas.
I appreciate any feedback, questions or improvements that you may have.









